 Click logo to return to 'links-page'
Click logo to return to 'links-page'
Music tones for String Animation Below
Links to audible frequencies here
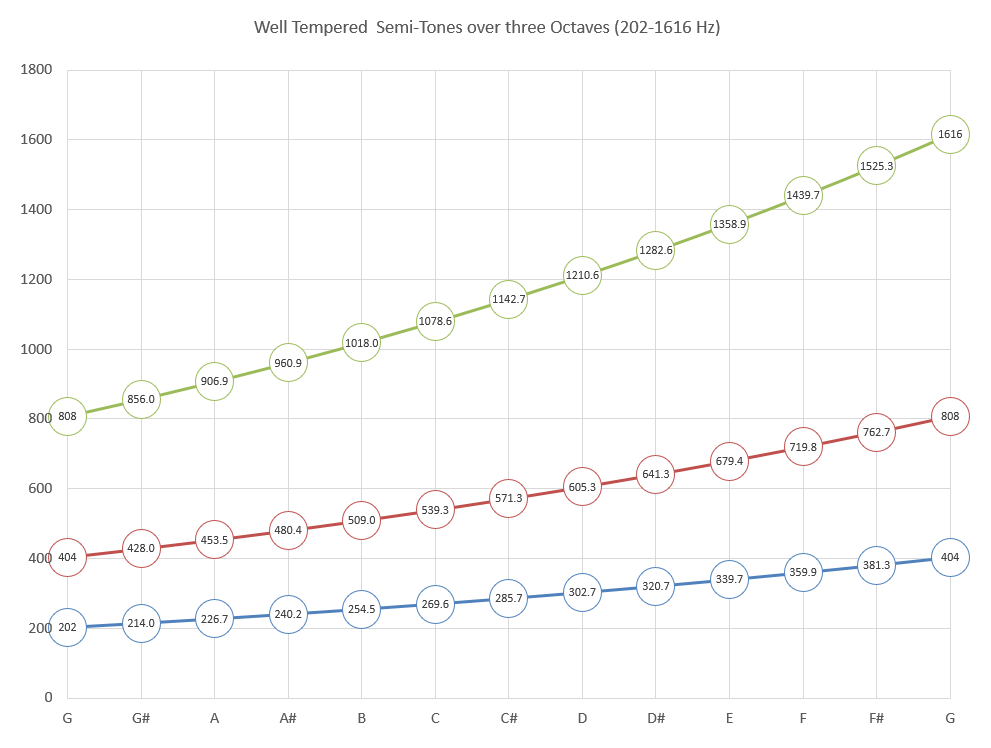
Structured Calculations for Well-Tempered Semi-Tones over three octaves
1 2 3 4 5 6 7 8 9 10 11 12 13 Semi-tones C C# D D# E F F# G G# A A# B C Well-tempered 1.000 1.059 1.122 1.189 1.260 1.335 1.414 1.498 1.587 1.682 1.782 1.888 2.000 2^(1/12) 202 214.0 226.7 240.2 254.5 269.6 285.7 302.7 320.7 339.7 359.9 381.3 404 1.059 404 428.0 453.5 480.4 509.0 539.3 571.3 605.3 641.3 679.4 719.8 762.7 808 808 856.0 906.9 960.9 1018.0 1078.6 1142.7 1210.6 1282.6 1358.9 1439.7 1525.3 1616 Click image below to get user-chooser control of both seeing-&-hearing the calculations animated
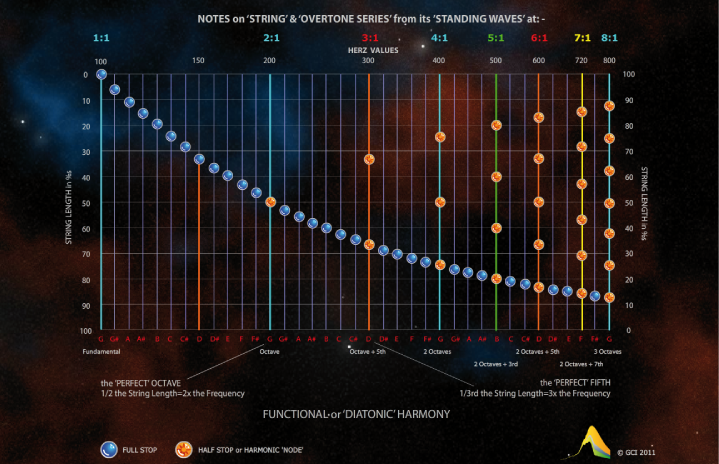
Pythagoras’ ‘law’ is revealed in a string at constant tension and length, as in the cello G-String shown here for example.
The image has Hz values based on G'0'=100 Hz, which is equivalent to a Cello G-String.
Here, Herz values have been slowed visually by a factor of 100, so the Herz doubling for the octave and trebling for the fifth [etc]
can more easily be ‘seen’ as well as 'heard' [as 'doublings', treblings' etc].
Click on the strings-picture below to animate as an andio-visual with user controls.
The audio-visual file for this is also here.
Once in the animation, mouse-touching buttons [one click ‘on’, second click ‘off’] AV animates each string.
The user controls of the animation enable any combination-progression within octave:12 semi-tone 'tonality'.
The sounds and sights of harmonic progressions are a click away.
- The gold-coloured buttons in the image to both hear and see how the ‘harmonics’ of the whole string,
or the ‘overtone series’, emerges ‘harmoniously’ from the ‘fundamental’ G.
- The blue-coloured buttons for ‘chromatic’ notes in between are not ‘harmonics’ in the first three octave,
but as whole numbers become harmonics in higher octaves.