David Bohm

Click logo to return to 'links-page'



From ‘Wholeness & the Implicate Order’ - David Bohm

“It is thus implied that measure is a form of insight into the essence of
everything, and that man’s perception, following on ways indicated by such
insight, will be clear and will thus bring about generally orderly action and
harmonious living. In this connection, it is useful to call to mind Ancient Greek
notions of measure in music and in the visual arts.

These notions emphasized that a grasp of measure was a key to the
understanding of harmony in music (e.g., measure as rhythm, right proportion
in intensity of sound, right proportion in tonality, etc.). Likewise, in the visual
arts, right measure was seen as essential to overall harmony and beauty (e.g.,
consider the ‘Golden Mean’; (often referred to as ‘Phi’).

All of this indicates how far the notion of measure went beyond that of
comparison with an external standard, to point to a universal sort of inner ratio
or proportion, perceived both through the senses and through the mind.
Of course, as time went on, this notion of measure gradually began to change,
to lose its subtlety and to become relatively gross and mechanical. Probably this
was because man’s notion of measure became more and more routinized and
habitual, both with regard to its outward display in measurements relative to an
external unit and to its inner significance as universal ratio relevant to physical
health, social order, and mental harmony.

Men began to learn such notions of measure mechanically, by fragmentation
and wholeness conforming to the teachings of their elders or their masters, and
not creatively through an inner feeling and understanding of the deeper
meaning of the ratio or proportion which they were learning.

So measure gradually came to be taught as a sort of rule that was to be imposed
from outside on the human being, who in turn imposed the corresponding
measure physically, socially and mentally, in every context in which he was
working.

As a result, the prevailing notions of measure were no longer seen as forms of
insight. Rather, they appeared to be ‘absolute truths about reality as it is’, which
men seemed always to have known, and whose origin was often explained
mythologically as binding injunctions of the Gods, which it would be both
dangerous and wicked to question.

Thought about measure thus tended to fall mainly into the domain of
unconscious habit and, as a result, the forms induced in perception by this
thought were now seen as directly observed objective realities, which were
essentially independent of how they were thought about.

Even by the time of the Ancient Greeks, this process had gone a long way and,
as men realized this, they began to question the notion of measure. Thus
Protagoras said: ‘Man is the measure of all things’, thus emphasizing that
measure is not a reality external to man, existing independently of him. But
many who were in the habit of looking at everything externally also applied this
way of looking to what Protagoras said. Thus, they concluded that measure was
something arbitrary, and subject to the capricious choice or taste of each
individual.

In this way they of course overlooked the fact that measure is a form of insight
that has to fit the overall reality in which man lives, as demonstrated by the
clarity of perception and harmony of action to which it leads. Such insight can
arise properly only when a man works with seriousness and honesty, putting
truth and factuality first, rather than his own whims or desires.”
http://www.gci.org.uk/movies/Perfect_Cadence.mp4

From ‘nothingness’ (0) to ‘somethingness’ at Phi (0.618) & back . . .
"das ewige geliebter zieht uns hinan."


David Bohm

The Implicate Order

Three-in-One 'Stringularity' helps to quantify Bohm's Implicate Order'.

e 

Based on the core structure of the hemiola, all life aspires to and flows from the condition of music.

With the collapse of 'perceptions' and probabilities, we could say, 'listen-up and calculate'.
This means the structure of moments & momentum, consciousness and feedback.

Here is how stringularity works out so far . . . .

The Higgs particle and the DNA molecule have suggestively been called the god-particle (Higgs) and the god-molecule (DNA);

We don't need to believe or disbelieve in god to increase understanding of this. We are no less inclined to be 'reverential' for observing this either.
In other words, dis/belief can distract from an understanding, which may increase as it is realized that the a/theist argument is self-referential,
i.e. trinity is integrated in stringularity, where the observed & the observer are one. There is no dichotomy, let alone one that is 'false'.

Some detail 

The Well Tempered Climate Accord was developed from these unifying principles.

**********************************************************

Here is a first pass at writing a publishable paper on 'The Stringularity Hypothesis' . . . .

The ‘Stringularity’ Hypothesis

How Pythagoras' simple string experiment, conducted in Crotone around 530 BC,
embeds a per-unit-time-based-derivation of the beautiful and irrational 'Phi'.

************************************************************************

The value of ‘Phi’ (.618…) is irrational. It is commonly derived from a ‘quadratic equation’
((the square root of 5 + 1)/2) of the Fibonacci Series (as in the Pentagon:Pentangle).

However, the value of ‘Phi’ can be quantized per-unit-time (Hz) from measuring and back-feeding
the differences in the phenomenon known as the ‘Pythagorean Comma’. Derived from ‘Stringularity’,
‘Phi’ is a point on a curve at the ‘Phi-point’, between steps 12 and 13 of the Pythagorean Comma.

It is constant anywhere from nano-to-macroscale. So, using the derivation of ‘Phi’ as a function of
steps per-unit-time, can be a relevant step in changing the cognitive paradigm where particles in
wave-fields are only probability perceptions still regarded as the ‘quantum measurement problem’.

********************************************************************

The ‘Stringularity’ Hypothesis; the ‘path-integral’ of Pythagoras’ String Experiment

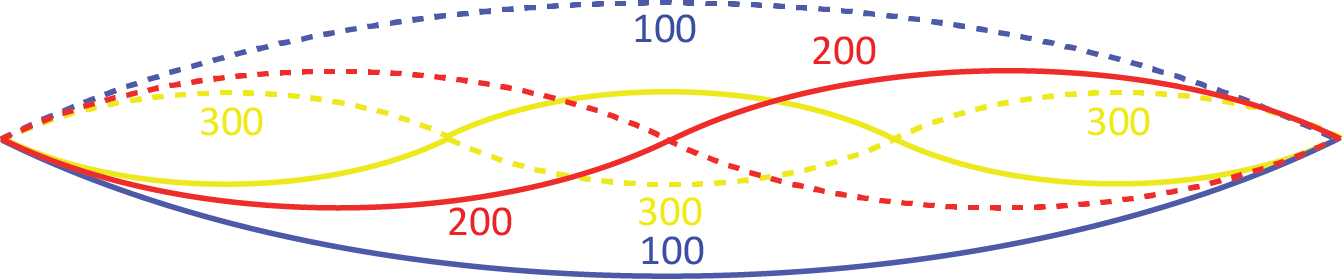
The now famous string experiment of Pythagoras (~ 530 BCE) demonstrates that: -

  1. When we take a string of constant length and constant tension tuned at 100 Hz
  2. And halve the length of the string, the frequency (Hz) doubles from 100 Hz to 200 Hz
  3. And that if we third the length of the string the frequency (Hz) trebles to 300 Hz etc . . . .

As the path-integral basis of the universally constant ‘harmonic series’, these steps start with: -

  1. the ‘Fundamental’
  2. the ‘Perfect Octave’
  3. the ‘Perfect Octave plus the Perfect Fifth’ etc . . . .

The Pythagorean Comma (see chart above)

Proceeding from above, the Pythagorean Comma emerges as a growing ‘gap’: -

  1. when we sequence seven ‘Perfect Octaves’ in Hertz (Hz), in the example shown we go through
    seven doublings 1 (each enlarging at 200%), from 100 Hz to 12,800.00 Hz,

  2. when we sequence twelve ‘Perfect Fifths’ we go in the example shown we go through 12 steps
    (each enlarging at 150%) from 100 Hz to 12,974.63 Hz,

  3. it becomes clear that seven Perfect Octaves (12,800.00 Hz) do not ‘commute’ exactly with
    twelve ‘Perfect Fifths’ 12,974.63 Hz. At this ‘twelfth-step’, the gap is 174.63 Hz (1.345...%)

Well-Tempered Tuning (see chart above)

  1. In order to get the twelve Perfect Fifths to commute with the seven Perfect Octaves,
    the Perfect Fifths (enlarging at 150%) are ‘Well Tempered’, enlarging at 149.83070768…%)

  2. The result of adopting this procedure is that twelve Well-Tempered Fifths commute exactly
    with seven Perfect Octaves (at 12,800 Hz), giving rise to what is called 'Well Tempered Tuning' (3, 4,)

The Hz Differences between Perfect and Well-Tempered Fifths lead to ‘Phi’

  1. When step-by-step, we subtract 12 Well Tempered Fifths from 12 Perfect Fifths,
    a sequence of differences between the two paths is the result (see table final page),

  2. When step-by-step, we back feed these differences into the sequence, so the largest
    difference is divided into the smaller difference that precedes it etc . . . (see table final page),

  3. A twelve step sequence with negative curvature (concavity) is revealed, decreasing from
    0.615731…. just below the value of ‘Phi’, to 0.000 (see table final page),

  4. When we go one step further and start at the thirteenth step of the Pythagorean Comma,
    the difference is 283.62 Hz, yielding a value 0.6199396…. just above the value of ‘Phi.

‘Phi’ is exactly at the Phi-Point between per-unit-time steps 12 & 13 of the Pythagorean Comma

  1. The value of ‘Phi’ is on the overall curve at exactly the Phi-point between steps 12 and 13
    of the Pythagorean Comma (see table x4) http://www.gci.org.uk/movies/PC_12_13.mp4

  2. Exponential growth curves at 200% 150% and 149.83070768…% etc are positively governed
    by acceleration (convexity) and unfold without limit towards infinity.

  3. Path-integral to that, the growth curve to ‘Phi’, is governed by deceleration within the
    feedback limits or concavity that define it, countervailing the convexity of acceleration.

  4. Deriving the value of ‘Phi’ from measuring the path-integral per-unit-time/space of
    ‘Stringularity’ is distinct from the time-free quadratic equation and the Fibonacci Series.

  5. This path-integral procedure gives rise to an array of time-based features which suggest corroboration.

John Archibald Wheeler said, ”It is my opinion that everything must be based on a simple idea
and it is my opinion that this idea, once we have finally discovered it, will be so compelling, so beautiful,
that we will say to one another, yes, how could it have been any different.”

The beauty and the deceptive simplicity of ‘Phi’ underlies the structure, the sequencing,
the symmetry and the curvature of natural phenomena, from the nanoscale to the macroscale.

Could this musical-derivation of ‘Phi’ be a simple yet beautiful idea that helps to answer Erwin Schrodinger’s
famous question, ‘What is Life’? Might it underlie a ‘cognitive framework’ that would help better to understand
the wave:particle dichotomy, the path-integral complexity, the moment:momentum and life:death challenges
that will always face us?

Concomitant corroboration . . . . ?

  1. Phi squares the circle
  2. The equivalence of Phi and Pi
  3. ‘Phi’ Squares the Circle
  4. Phyllotaxis - the emergent and ubiquitous Phi
  5. The 'symmetry binding' properties of Hz-derived Phi integration
  6. the relevance of this to the Standard Model when introducing the Higgs Boson
  7. Phi-Spiral (vortex) 'black-holes' from excitons to galaxies

    Footnotes

1. Seven Perfect Octaves (or Hz doublings) is about the length of a modern grand-piano keyboard.

2. This ‘non-commutation’ phenomenon has been recognized for Millennia.
Unaffected by issues of scale and whatever base Hz value is set for ‘doublings,
if 12 Well Tempered Fifths are 100%, 12 Perfect Fifths are always 101.36433…%.

3. In musical narrative, the purpose of adopting ‘Well Tempering’ was to enable music
to be written and played in all the keys (of all the 12 semitone steps in the octave)
so they are all equally ‘in-tune’ and where modulating between these keys these is
smoothed by the equality of the twelve semitone steps in the Perfect Octaves arising.

4. The classical example of this is the Well-Tempered Clavier of JS Bach (1721).